GRAFOS

Un grafo, G, es un par ordenado de V y A, donde V es el conjunto de vértices o nodos del grafo y A es un conjunto de pares de vértices, a estos también se les llama arcos o ejes del grafo. Un vértice puede tener 0 o más aristas, pero toda arista debe unir exactamente a dos vértices.
Los grafos representan conjuntos de objetos que no tienen restricción de relación entre ellos. Un grafo puede representar varias cosas de la realidad cotidiana, tales como mapas de carreteras, vías férreas, circuitos eléctricos, etc.
La notación G = A (V, A) se utiliza comúnmente para identificar un grafo.
Los grafos se constituyen principalmente de dos partes: las aristas, vértices y los caminos que pueda contener el mismo grafo.
Aristas

Son las líneas con las que se unen las aristas de un grafo y con la que se construyen también caminos.
Si la arista carece de dirección se denota indistintamente {a, b} o {b, a}, siendo a y b los vértices que une.
Si {a ,b} es una arista, a los vértices a y b se les llama sus extremos.

Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.
Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.
Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.
Cruce: Son dos aristas que cruzan en un punto.

Vértices

Son los puntos o nodos con los que esta conformado un grafo.
Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un vértice es `par' o `impar' según lo sea su grado.

Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
Vértice Aislado: Es un vértice de grado cero.
Vértice Terminal: Es un vértice de grado 1.

Caminos
Sean x, y " V, se dice que hay un camino en G de x a y si existe una sucesión finita no vacía de aristas {x,v1}, {v1,v2},..., {vn,y}. En este caso

x e y se llaman los extremos del camino
El número de aristas del camino se llama la longitud del camino.
Si los vértices no se repiten el camino se dice propio o simple.
Si hay un camino no simple entre 2 vértices, también habrá un camino simple entre ellos.
Cuando los dos extremos de un camino son iguales, el camino se llama circuito o camino cerrado.
Llamaremos ciclo a un circuito simple
Un vértice a se dice accesible desde el vértice b si existe un camino entre ellos. Todo vértice es accesible respecto a si mismo

CLASIFICACION DE GRAFOS

Podemos clasificar los grafos en dos grupos: dirigidos y no dirigidos. En un grafo no dirigido el par de vértices que representa un arco no está ordenado. Por lo tanto, los pares (v1, v2) y (v2, v1) representan el mismo arco. En un grafo dirigido cada arco está representado por un par ordenado de vértices, de forma que y representan dos arcos diferentes.
Ejemplos
G1 = (V1, A1)
V1 = {1, 2, 3, 4} A1 = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}
G2 = (V2, A2)
V2 = {1, 2, 3, 4, 5, 6} A2 = {(1, 2), (1, 3), (2, 4), (2, 5), (3, 6)}
G3 = (V3, A3)
V3 = {1, 2, 3} A3 = { <1, 2>, <2, 1>, <2, 3> }
Gráficamente estas tres estructuras de vértices y arcos se pueden representar de la siguiente manera:

Algunos de los principales tipos de grafos son los que se muestran a continuación:

Grafo regular: Aquel con el mismo grado en todos los vértices. Si ese grado es k lo llamaremos k-regular.
Por ejemplo, el primero de los siguientes grafos es 3-regular, el segundo es 2-regular y el tercero no es regular

Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto
Ejemplo.- de los dos grafos siguientes el primero es bipartito y el segundo no lo es

Grafo completo: Aquel con una arista entre cada par de vértices. Un grafo completo con n vértices se denota Kn.

A continuación pueden verse los dibujos de K3, K4, K5 y K6

Un grafo bipartito regular: se denota Km,n donde m, n es el grado de cada conjunto disjunto de vértices.
A continuación ponemos los dibujos de K1,2, K3,3, y K2,5

Grafo nulo: Se dice que un grafo es nulo cuando los vértices que lo componen no están conectados, esto es, que son vértices aislados.

Grafos Isomorfos: Dos grafos son isomorfos cuando existe una correspondencia biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan unidos por una arista en común.

Grafos Platónicos: Son los Grafos formados por los vértices y aristas de los cinco sólidos regulares (Sólidos Platónicos), a saber, el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.

GRAFOS EULERIANOS.
Para definir un camino euleriano es importante definir un camino euleriano primero. Un camino euleriano se define de la manera más sencilla como un camino que contiene todos los arcos del grafo.
Teniendo esto definido podemos hablar de los grafos eulerianos describiéndolos simplemente como aquel grafo que contiene un camino euleriano. Como ejemplos tenemos las siguientes imágenes:

El primer grafo de ellos no contiene caminos eulerianos mientras el segundo contiene al menos uno.
GRAFOS CONEXOS.
Un grafo se puede definir como conexo si cualquier vértice V pertenece al conjunto de vértices y es alcanzable por algún otro. Otra definición que dejaría esto más claro sería: “un grafo conexo es un grafo no dirigido de modo que para cualquier par de nodos existe al menos un camino que los une”.

Representación matricial

Un número complejo se puede representar como un vector y un vector como matriz,por lo que suena lógico que un número complejo se pueda representar con una matriz, sólo que la representación no tiene que ser propiamente la de un vector en una matriz. Una posible representación de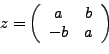 $z \in \mathbb{R}$ con

$\begin{displaymath} z = \left( \begin{array}{ccc} a & b \\ -b & a \end{array}\right) \end{displaymath}$

El primer renglón nos dará el número complejo. Podemos definir la unidad real como

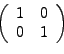
$\begin{displaymath} \left( \begin{array}{cccc} 1 & 0 \\ 0 & 1 \end{array}\right) \end{displaymath}$

y la imaginaria como

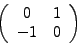
$\begin{displaymath} \left( \begin{array}{cccc} 0 & 1 \\ -1 & 0 \end{array}\right) \end{displaymath}$

al ser un número complejo la suma de un número real más otro número real por la unidad imaginaria, podemos hacerlo matricialmene

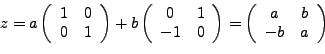
$\begin{displaymath} z =a \left( \begin{array}{cccc} 1 & 0 \\ 0 & 1 \end{arra... ...ft( \begin{array}{cccc} a & b \\ -b & a \end{array}\right) \end{displaymath}$

Con esta representación la aritmetica compleja es isomorfa a las operaciones con matrices.

Caminos y circuitos.

Camino.
Es una sucesión de lados que van de un nodo x a un nodo w (dichos lados se pueden repetir).

Circuito o ciclo.
Es un camino del nodo w al nodo w, esto es, un camino que regresa al mismo nodo de donde salió.

Circuito simple de longitud n.
Es aquel camino del nodo w al nodo w que solamente tiene un ciclo en la ruta que sigue.

Camino simple de longitud n.
Es una sucesión de lados que van de un nodo x a un nodo w, en donde los lados que componen dicho camino son distintos e iguales a n. Esto significa que no se puede pasar dos veces por una misma arista.

Camino de Euler.
Es aquel camino que recorre todos los nodos pasando por todas las aristas solamente una vez. Una característica importante de los grafos que tienen camino de Euler es que siempre comienzan y terminan en nodos que terminan en valencia impar.

Circuito de Euler.
Es aquel ciclo que recorre todos los nodos pasando por todos las aristas solamente una vez.
Un grafo tiene un Circuito de Euler si y solo si es conexo y todos sus nodos tienen valencia par.

Algoritmo de Fleury.
Nos permite determinar un circuito de Euler:
1)Verificar que el grafo sea conexo y que todos los nodos tengan valencia par. Si no cumple el grafo no tiene circuito de Euler y finalizar.
2)Si cumple con la condición anterior, seleccionar un nodo arbitrario para iniciar el recorrido.
3)Escoger una arista a partir del nodo actual. Esa arista seleccionada no debe de ser “lado puente”, a menos que no exista otra opción.
4)Desconectar los nodos que están unidos por la arista seleccionada.
5)Si todos los nodos del grafo ya estan desconectados, ya se tiene un circuito de Euler y finalizar. De otra manera continuar con el paso 3.

En el siglo XX se ha precisado en matemáticas la noción intuitiva de estructura, siguiendo la concepción de Aristóteles de la materia y la forma, según la cual cada estructura es un conjunto X dotado de ciertas operaciones (como la suma o el producto), o de ciertas relaciones (como una ordenación) o ciertos subconjuntos (como en el caso de la topología), etc. En este caso el conjunto X es la materia y las operaciones, relaciones, etc., en él definidas, son la forma.

Ejemplos de Isomorfismos Por ejemplo, si X es un números real positivo con el producto e Y es un número real con la suma, el logaritmo ln:X→Y es un isomorfismo, porque ln(ab)=ln(a)+ln(b) y cada número real es el logaritmo de un único número real positivo. Esto significa que cada enunciado sobre el producto de números reales positivos tiene (sin más que sustituir cada número por su logaritmo) un enunciado equivalente en términos de la suma de números reales, que suele ser más simple.

Otro ejemplo: si en el espacio E elegimos una unidad de longitud y tres ejes mutuamente perpendiculares que concurren en un punto, entonces a cada punto del espacio podemos asociarles sus tres coordenadas cartesianas, obteniendo así una aplicación f:E→R³ en el conjunto de las sucesiones de tres números reales. Cuando en E consideramos la distancia que define la unidad de longitud fijada y en R³ consideramos la distancia que define la raíz cuadrada de la suma de los cuadrados de las diferencias, f es un isomorfismo. Éste descubrimiento fundamental de Descartes permite enunciar cualquier problema de la geometría del espacio en términos de sucesiones de tres números reales, y este método de abordar los problemas geométricos es el corazón de la llamada geometría analítica.

Características del Isomorfismo

El descubrimiento de Platón de que la forma es lo que importa se recoge en matemáticas con el concepto de isomorfismo. Una aplicación f:X→Y entre dos conjuntos dotados del mismo tipo de estructura es un isomorfismo cuando cada elemento de Y proviene de un único elemento de X y f transforma las operaciones, relaciones, etc. que hay en X en las que hay en Y. Cuando entre dos estructuras hay un isomorfismo, ambas son indistinguibles, tienen las mismas propiedades, y cualquier enunciado es simultáneamente cierto o falso. Por eso en matemáticas las estructuras deben clasificarse salvo isomorfismos. Ejemplos de Isomorfismos Por ejemplo, si X es un números real positivo con el producto e Y es un número real con la suma, el logaritmo ln:X→Y es un isomorfismo, porque ln(ab)=ln(a)+ln(b) y cada número real es el logaritmo de un único número real positivo. Esto significa que cada enunciado sobre el producto de números reales positivos tiene (sin más que sustituir cada número por su logaritmo) un enunciado equivalente en términos de la suma de números reales, que suele ser más simple.

Características del Isomorfismo El descubrimiento de un isomorfismo entre dos estructuras significa esencialmente que el estudio de cada una puede reducirse al de la otra, lo que nos da dos puntos de vista diferentes sobre cada cuestión y suele ser esencial en su adecuada comprensión. También significa una analogía como una forma de inferencia lógica basada en la asunción de que dos cosas son la misma en algunos aspectos, aquellos sobre los que está hecha la comparación. En ciencias sociales la aplicación de una ley análoga por no existir una específica o también la comparación de un sistema biológico con un sistema social, cuando se trata definir la palabra sistema. Lo es igualmente la imitación o copia de una estructura tribal en un hábitat con estructura urbana.

Los morfismos Los isomorfismos de una estructura consigo misma se denominan automorfismos. En general, en una categoría arbitraria, los isomorfismos se definen por ser los morfismos f:X→Y que admiten un morfismo inverso h:Y→X, inverso tanto por la derecha como por la izquierda. Pueden no ser los morfismos biyectivos, como ya ocurre en el caso de los espacios topológicos.

Publicado por Juan Ramirez Lopez

ISOMORFISMO

Matilde Aldava Herrera

Dados G=(V,E) y G´=(V´,E´), se denomina isomorfismo de G a G´ a la aplicación biyectiva f tal que para a,bÎV, {a,b}ÎE Û se cumple {f(a),f(b)}ÎE´. Es decir, la aplicación que relaciona biyectivamente pares de vértices de E con pares de vértices de E´, de modo que los vértices conectados por aristas siguen estándolo.

G y G´ se denominan isomorfos, y son matemáticamente iguales, solo varia la apariencia, o sea, que se mantienen las adyacencias, estructura, caminos y ciclos.

Los grafos G y G ‘ son isomorfos pues existe la biyección f: V ® V ‘ definida por f(a) = 2, f(b) = 1, f© = 3, f(d) = 4 que conserva la adyacencia.

Complejidad

Los problemas matemáticos se pueden dividir en primera instancia en dos grupos

      Problemas indecidibles: aquellos que no se pueden resolver mediante un algoritmo.

Ø Problemas decidibles: aquellos que cuentan al menos con un algoritmo para su cómputo.

Sin embargo, que un problema sea decidible no implica que se pueda encontrar su solución, pues muchos problemas que disponen de algoritmos para su resolución son inabordables para un computador por el elevado número de operaciones que hay que realizar para resolverlos. Esto permite separar los problemas decidibles en dos:

Ø intratables: aquellos para los que no es factible obtener su solución.

Ø tratables: aquellos para los que existe al menos un algoritmo capaz de resolverlo en un tiempo razonable.

Los problemas pueden clasificarse también atendiendo a su complejidad. Aquellos problemas para los que se conoce un algoritmo polinómico que los resuelve se denominan clase P. Los algoritmos que los resuelven son deterministas. Para otros problemas, sus mejores algoritmos conocidos son no deterministas. Esta clase de problemas se denomina clase NP. Por tanto, los problemas de la clase P son un subconjunto de los de la clase NP, pues sólo cuentan con una alternativa en cada paso.

El problema de isomorfismo de grafos no se sabe si es un problema de la clase P o de la clase NP, y si hubiese una clase intermedia entre ambas, el isomorfismo de grafos sería el tipo de problema ideal para ella.

Existe un caso concreto de grafos (los árboles) donde el problema del isomorfismo si se puede resolver mediante la aplicación de algoritmos no muy complejos.

Grafo plano

Grafos de ejemplo
Plano	No plano
	K₅
El grafo completo K₄ es plano	K_3,3

Definición y ejemplos

En teoría de grafos, un grafo plano (o planar según referencias) es un grafo que puede ser dibujado en el plano sin que ninguna arista se interseque (una definición más formal puede ser que este grafo pueda ser "embebido" en un plano). Un grafo no es plano si no puede ser dibujado sobre un plano sin que sus aristas se intersequen. Los grafos K₅ y el K_3,3 son los grafos no planos minimales, lo cual nos permitirán caracterizar el resto de los grafos no planos.

Teorema de Kuratowski

El matemático polaco Kazimierz Kuratowski encontró una caracterización de los grafos planos, conocida como el teorema de Kuratowski:

Un grafo es plano si y solo si no contiene un subgrafo que es una subdivisión elemental de K₅ (el grafo completo de 5 vértices) o K_3,3 (el grafo bipartito completo de 6 vértices).

Una subdivisión elemental de un grafo resulta de insertar vértices en las aristas (por ejemplo, cambiando •——• por •—•—•). Una formulación equivalente a este teorema es:

Un grafo es plano sí y solo sí no contiene ningún subgrafo homeomorfo a K₅ ó K_3,3.

Otros criterios para determinar si un grafo es plano

En la práctica, es difícil usar el teorema de Kuratowski para decidir rápidamente si un grafo es plano. Sin embargo, existe un algoritmo rápido para este problema: dado un grafo de n vértices y e el número de aristas, es posible determinar en tiempo O(n) (lineal) si el grafo es plano o no, utilizando los dos teoremas siguientes:

Teorema 1. Si n ≥ 3 entonces e ≤ 3n - 6

Teorema 2. Si n > 3 y no existen ciclos de longitud 3, entonces e ≤ 2n - 4

El grafo K_3,3, por ejemplo, tiene 6 vértices, 9 aristas y ningún ciclo de longitud 3. Por el teorema 2, no puede ser plano. Nótese que estos teoremas están construidos con una implicación unidireccional (si), y no bicondicional (si y solo si) y por tanto, solamente pueden ser usados para probar que el grafo no es plano, pero no que sea plano. Si ambos teoremas fallan, deben usarse otros métodos.

Fórmula de Euler

La fórmula de Euler enuncia que si un grafo conexo, plano es dibujado sobre un plano sin intersección de aristas, y siendo v el número de vértices, e el de aristas y f la cantidad de caras (regiones conectadas por aristas, incluyendo la región externa e infinita), entonces:

v − e + f = 2,

Por ejemplo, la Característica de Euler es 2. De manera más ilustrativa, en los ejemplos anteriores, en el primer grafo plano tenemos: v=6, e=7 y f=3. Si el segundo grafo se redibuja sin las intersecciones de aristas, tenemos v=4, e=6 y f=4. La fórmula de Euler se puede probar de la siguiente manera: si el grafo no es un árbol, entonces se elimina una arista que completa un ciclo. Esto disminuye el valor de e y f en uno, dejando v − e + f constante. Repítase hasta llegar a un árbol. Los árboles tienen v = e + 1 y f = 1, verificando la fórmula v - e + f = 2.
En un grafo simple, conexo y plano, cualquier región (posiblemente exceptuando la exterior) está conectada por al menos tres aristas y cada arista toca como mucho dos regiones. Usando la fórmula de Euler, se puede demostrar que estos grafos son escasos en el sentido que e ≤ 3v - 6 si v ≥ 3.
Se le dice plano maximal al grafo que es plano pero al agregarle cualquier arista dejase de serlo. Todas las regiones (incluso la externa) están conectadas por tres aristas, explicando la definición alternativa de triangular para este tipo de grafos. Si un grafo triangular tiene v vértices con v > 2, entonces tiene exactamente 3v - 6 aristas y 2v - 4 regiones.
Nótese que la fórmulta de Euler también es válida para poliedros simples. No es una casualidad: cada poliedro simple se puede ver como un grafo plano y conexo usando los vértices del poliedro como vértices del grafo, y las aristas del poliedro como aristas del grafo. Las caras o regiones del grafo plano resultante corresponden a las caras del poliedro. Por ejemplo, el segundo grafo plano del ejemplo corresponde a un tetraedro. Alternativamente, no todos los grafos planos y simples corresponden a un poliedro (los árboles, por ejemplo). Un teorema de Ernst Steinitz dice que los grafos planos formados a partir de poliedros convexos son precisamente los grafos planos simples y triangulares.